July 11, 2016
Understanding the depth in deep learning through the lense of chaos theory¶
Chetan Nichkawde¶
The age of machines has dawned with the promise to understand all physical and human phenomenon by employing intelligent machines. These machines harvest a repertoire of neurons that encode the mechanisms of these systems and thus faithfully represent the system itself. These promises to impart us premonition capabilities and help make intelligent decisions. The forerunner among all such artificially intelligent systems are deep neural network. MIT technology review is listed it as most disruptive technology in the 21st century. The process of creation of such artificial neural network has been termed as deep learning. The term deep in deep learning refers to multiple layers of neuron ensemble stacked one after the other. Conversely, a shallow network is a neural network with just one layer between the input and the output. The cognitive abilities of deep neural network have been attributed to it's depth. This post uncovers some of the mysteries behind the role of depth in imparting such abilities.
This post has been written for a reader with minimal background in machine learning. However, a reader with advanced knowledge will also feel benefited.
A brief history of chaos theory¶
The story of depth is intimately interlinked with the story of chaos theory and begins in the decade of 60s when Edward Lorenz, a physicist at MIT atmospheric sciences, discovered that time evolution of the states for a model for atmospheric dynamics shows extreme sensitivity to the initial condition (starting point). We will understand later that how time evolution is connected to depth in a feedforward neural network. Thus if you start at a point with decimal points difference from another point you will end up at a completely different point after some time. This phenomenon is also known as butterfly effect.

In the picture above, the future position of the moving ball is extremely sensitive to it's starting point. Move the initial point of the ball a tinge and it will end at a completely different place on the butterfly wings after only few time steps.

This is also illustrated in the picture above. The blue cone and the yellow are initially co-located differing only by $10^{-5}$ in the $x$-coordinate. After only 30 time steps, they end up at a completely different position. This exponential divergence of trajectories is one of the fundamental property of a chaotic dynamical system. The more chaotic the system, the more rapidly the trajectories will diverge. This is quantified in terms of Lyapunov exponent. We will revisit this figure later in this post. Let's call this Figure 1.
(Side note -- the long term collection of states over which the system evolves is termed as attractor and the dynamics is ergodic on the attractor. Markov chain Monte Carlo algorithm which is used to sample a probability distribution constructs a Markov chain whose attractor is ergodic on the joint distribution which we want to sample.)
Enter neural network¶
Can a neural network be chaotic? The answer is an emphatic yes. But wait, what does it even mean for a neural network to be chaotic? Let us first understand what is a neural network. The neural network is collection of neurons. Each of these neurons has their own state. The $x$, $y$ and $z$ variables in Lorenz system could, for example, represent the state of a neural network with just 3 neurons. The states of the neuron can evolve time wise like in Lorenz system. In a dynamical system like Lorenz, the next state is a function of the current state. This is known as Markov property.
So here we come to core idea -- the next state in time is analogous to the state of the next layer in a deep network.
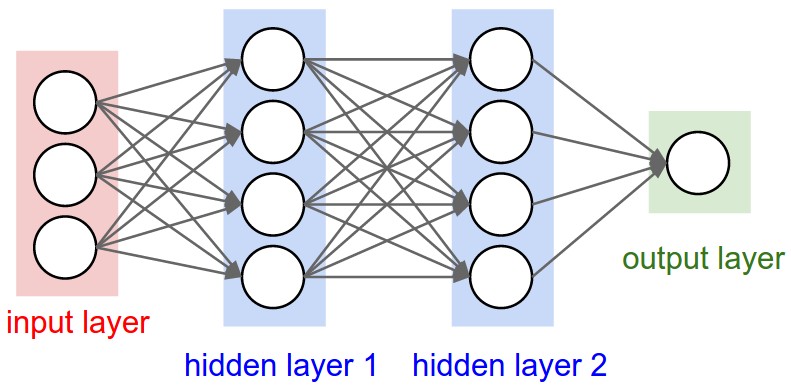
The figure above shows a feedforward network with two hidden layers. The states of 4 neurons in the hidden layer 1 feed as input to the hidden layer 2 and is instrumental in determining the states of 4 neurons in the hidden layer 2. One can also think of layer 2 as the next state in time of layer 1 and layer 3 as the next state in time of layer 2 and so on ..... Now, what happens if each layer is chaotic? Very small changes in the state of layer 1 would result in a completely different state of layer 2! Similarly, a small change in the input will result in a completely different state of layer 1. We will understand later why this is a desirable thing and how it helps us model complex systems.
A statistical physics magic¶

A 1988 work by Sompolinsky et al published in PRL showed that a sufficiently large sized neural network can indeed become chaotic if it's parameters are carefully tuned. They employed a certain statistical physics magic known as mean field approximation to show that a large sized network can become chaotic in a particular parameter regime.
Why make it deep?¶
Even a neural network with a single layer is a universal function approximator. Ingrid Daubechies wrote in recent article:
Decades ago, researchers proved that these networks are universal, meaning that they can generate all possible functions. Other researchers later proved a number of theoretical results about the unique correspondence between a network and the function it generates. But these results assume networks that can have extremely large numbers of layers and of function nodes within each layer. In practice, neural networks use anywhere between two and two dozen layers. Because of this limitation, none of the classical results come close to explaining why neural networks and deep learning work as spectacularly well as they do.
This means that in theory at least they can be used to model any system. So then why make it deep? Let's understand how depth imparts greater modeling ability with lesser resources.

Consider two input data points represented by the red star and blue star in the figure above. Although they are very very close in the input space, they have a very different correlation with the output. For instance, these two data points could belong to two different classes. There could be many such spots on our data manifold where nearby points map to completely different regions in the output space. A neural network is supposed to comprehend this and separate them. Now let's think of single layer network. We could in principle model this just using a single layer with a very large number of neurons. The network should be able separate the red and blue star in a manner similar to separating the two nearby trajectories, differing only by $10^{-5}$ in Figure 1. Remember the blue cone and the yellow cone in Figure 1 showed visible separation only after 30 time steps. They are still indistinguishable from each other after only 1 time step. Thus, even if we somehow achieve a large Lyapunov exponent, there is a limit to how much we can separate in a single time step or analogously a single layer. Now what we if increase the depth of the network and stack multiple layers in front of each other. The beam of input diverges as they pass through each chaotic lens and we can see a clear separation in the final projection on the screen of output. This has been illustrated in the figure above. This is similar to the blue cone and the yellow cone having clear separation after 30 steps.
So here is another big idea -- training of deep neural network involves tuning parameters so that each layer is optimally chaotic to accomplish a particular task.
(I welcome questions and comments. Please write to me at chetan.nichkawde@gmail.com.)